خطاهای ناشی از عدم همراستایی گیج در جهت مورد نظر
اگر استرین گیج در راستای محور مورد نظر به درستی نصب نشود، باعث بروز خطاهایی در نشانگر خواهد شد، در این مقاله با این خطاها آشنا خواهید شد

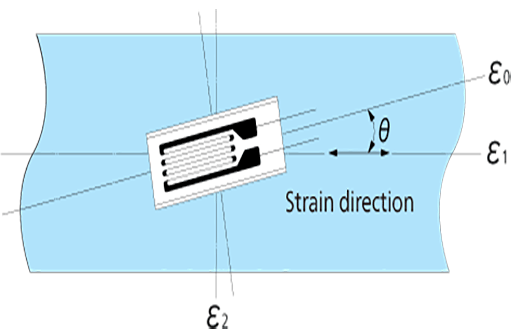
اگر استرین گیج در راستای محور مورد نظر به درستی نصب نشود، باعث بروز خطاهایی در نشانگر خواهد شد، در این مقاله با این خطاها آشنا خواهید شد


هنگامی که یک گیج با یک خطای زاویه ای کوچک با توجه به محور اندازه گیری کرنش مورد نظر به سطح جسم تحت تست متصل می شود، کرنش نشان داده شده نیز به دلیل عدم نصب صحیح گیج با خطا همراه خواهد بود. به طور کلی، برای یک گیج تکی در یک میدان کرنش تک محوری یکنواخت، بزرگی خطای ناهمترازی به سه عامل بستگی دارد (بدون توجه به حساسیت عرضی):
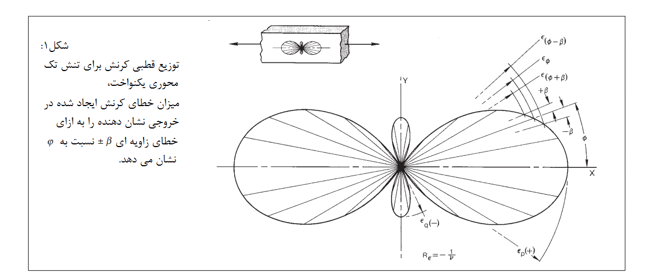
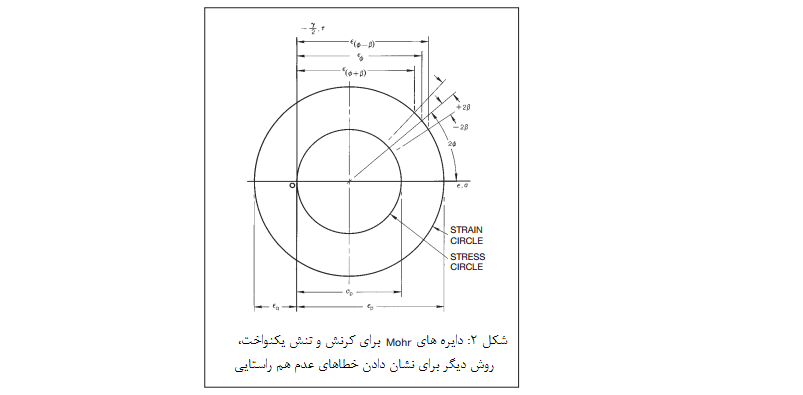
این مقادیر در شکلهای 1 و 2 برای حالت خاص اما رایج تنش تک محوری تعریف شدهاند. شکل 1 نمودار قطبی کرنش در نقطه مورد نظر است و شکل 2 دایره های Mohr متحدالمرکز را برای تنش و کرنش برای همان نقطه نشان می دهد. در شکل 1، فاصله تا مرز نمودار در امتداد هر خط شعاعی متناسب با کرنش عمود در امتداد همان خط است. لوب های کوچک در امتداد محور Y در نمودار نشان دهنده کرنش پواسون منفی برای این مورد است. از شکل 1 می توان به صورت کیفی مشاهده کرد که وقتی 0 ϕ یا 90 درجه باشد، یک خطای کوچک زاویه ای نصب گیج، خطای بسیار ناچیزی در نشانگر کرنش ایجاد می کند، زیرا نمودار کرنش قطبی در این نقاط نسبتا صاف و هموار است و شب خطوط عبوری از این نقاط نیز صفر می باشد.
با این حال، برای زوایای بین 0 تا 90 درجه، شکل 1 نشان می دهد که خطا در کرنش نشان داده شده به دلیل خطای نصب زاویه ای کوچک، می تواند به طرز شگفت آوری بزرگ باشد زیرا شیب نمودار کرنش قطبی در این مناطق بسیار تند است. به طور مشخص تر، می توان از شکل 2 هنگامی که φ=45° ، یا 2φ=90° باشد، متوجه شد که خطای نصب کوچک زاویه ای حداکثر خطا را در کرنش نشان داده شده ایجاد می کند، زیرا ε در این نقاط با بیشترین سرعت نسبت به زاویه تغییر می کند. این موضوع را می توان به صورت تحلیلی با نوشتن معادلات کرنش برای دیاگرام مورد نظر نیز بدست آورد. بدین ترتیب که مشتق دوم معادلات را نسبت به زاویه برابر صفر قرار می دهیم و ریشه های آن را بدست می آوریم. در حالت کلی می توان نشان داد که بیشترین خطای به وجود آمده در اندازه گیری کرنش به دلیل عدم همراستایی گیج با محور مورد نظر، در φ=45° رخ می دهد. همچنین حداقل خطا در φ=0° رخ می دهد.
خطای کرنش ایجاد شده به دلیل عدم همراستایی محور گیج با محور مورد نظر به صورت رابطه زیر می باشد:
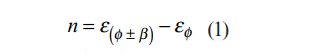
که در آن :
:n خطا بر حسب με
:εφ کرنش در راستای محور مورد نظر که با محور مولفه اصلی زاویه φ می سازد. و مقدار آن برحسب με در رابطه وارد می شود
:ε((φ±β)) کرنش در راستای محور گیج که با خطای زاویه ای β± نسبت به محور مورد نظر نصب شده است. و مقدار آن برحسب με در رابطه وارد می شود.
همچنین می توان از رابطه زیر نیز مقدار خطا را محاسبه کرد.
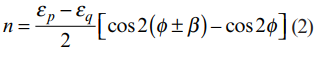
که در آن εpو εq به ترتیب ماکزیمم و مینیمم مولفه اصلی کرنش می باشند.
همچنین خطا را می توان بر حسب درصدی از εφ نیز نشان داد:
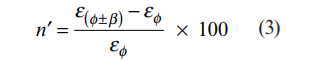
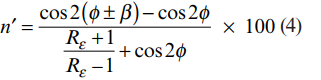
که در آن Rε=εp/εq می باشد.
با این وجود از رابطه (3) مشخص است که برای مقادیر کوچک εφ ، مقدار n به طور بی معنی بزرگ است. و زمانی که εφ صفر می شود، مقدار آن به بی نهایت میل می کند. برای بهتر نشان دادن میزان بزرگی خطای ناشی از عدم هم راستایی گیج در جهت مورد نظر، رابطه (2) را برای حالت های مختلف معمول، مورد ارزیابی قرار می دهیم.
خطای خزش و پسماند در استرین گیج ها
خزش و پسماند نقش مهمی در انتخاب گیج برای مبدل ها دارند در این مقاله شما با خطای خزش و همچنین خطای پسماند گیج های مختلف آشنا خواهید شد.

در یک میدان تنش تک محوره، εq=-vεp می باشد. همچنین برای استیل داریم v=0.285 . فرض کنید εp=1000με باشد در این صورت εq=-285με بدست می آید. و
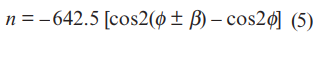
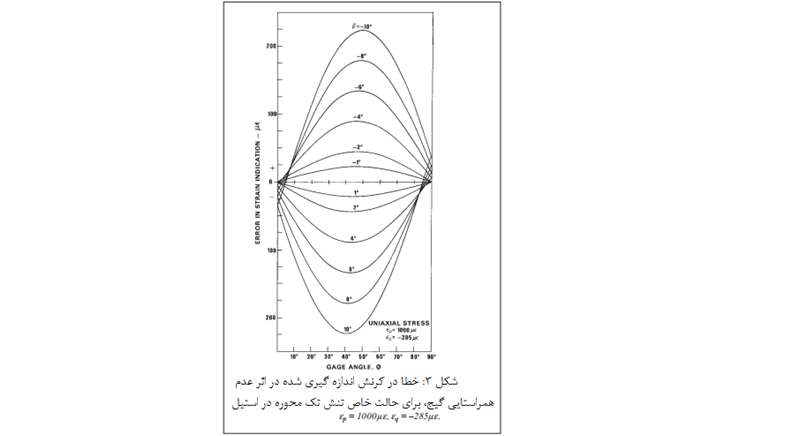
معادله (5) در شکل 3 برای مقادیر 0 تا 90 درجه φ، و همچنین زاویه خطای نصب در محدوده 0 الی 10 درجه رسم شده است.
برای تصحیح خطای ناشی از عدم هم راستایی گیج، برای یک زاویه معلوم، کافی است مقدار n را از شکل 3 بخوانید و در رابطه (1) جایگذاری کنید و رابطه (1) را برای εφ حل کنید.
این شکل فقط به عنوان مثال آورده شده است و فقط در موردی اعمال می شود که εq=-285με باشد(تنش تک محوری در فولاد). از رابطه (2) می توان برای ایجاد منحنی های خطای مشابه برای هر حالت کرنش دو محوری هم استفاده کرد.
مطالب بالا در مورد تجزیه و تحلیل خطاهای ناشی از عدم هم راستایی گیج در راستای مطلوب برای گیج های تکی، درک عمیقی از ماهیت چنین خطاهایی را برای کاربر به دست می دهد. اما در عمل معمولا روزت های دوگیجه مستطیلی بیشترین کاربرد را دارند.
یک روزت مستطیلی دو گیج معمولا توسط تحلیلگران تنش به منظور تعیین مولفه های اصلی تنشها ،زمانی که جهت محورهای اصلی از منابع دیگر مشخص است استفاده میشود. در این حالت، روزت باید طوری در جای خود چسبانده شود که محورهای گیج های آن در راستای محورهای اصلی تنش ها باشند. در این حالت به دلیل خطاهای ناشی از عدم نصب صحیح گیج در راستاهای مورد نظر و همچنین به خاطر عدم تعیین درست موقعیت محورهای اصلی تنش، خطاهای متناظر در تنش های اصلی که از قرائت کرنش ها محاسبه می شود، وجود خواهد داشت.
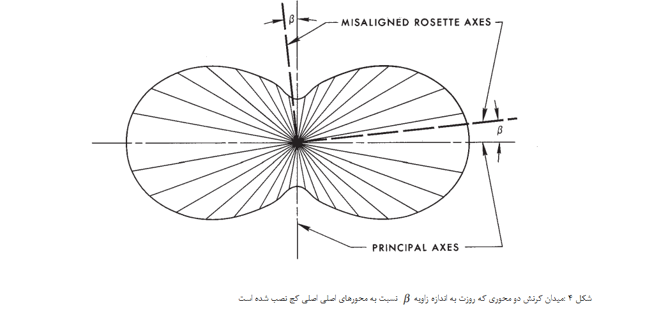
در شکل 4، یک میدان کرنش دو محوری کلی به همراه محورهای گیج های روزت که به مقدار زاویه β با محورهای اصلی کرنش نصب شده است، نشان داده شده است. درصد خطاهای تنش های اصلی و حداکثر تنش برشی ناشی از ناهمترازی عبارتند از:
پایه و اساس مدار پل وتستون و نحوه عملکرد آن
در این مقاله شما با نحوه عملکرد مدار پل وتستون به همراه روابط کامل آن در مبدل های استرین گیجی آشنا خواهید شد
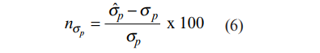
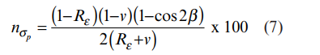
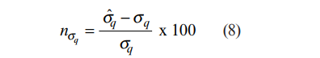
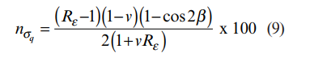
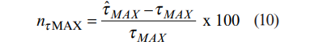
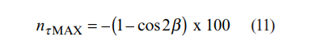
که در آن 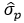 ،
،
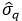 و
و 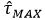 تنش های اصلی و ماکزیمم تنش برشی استخراج شده از قرائت کرنش های گیج ها، برای حالتی که روزت به اندازه زاویه
β نصب به محورهای اصلی کج نصب شده است.
تنش های اصلی و ماکزیمم تنش برشی استخراج شده از قرائت کرنش های گیج ها، برای حالتی که روزت به اندازه زاویه
β نصب به محورهای اصلی کج نصب شده است.
اگر نسبت تنش اصلی به جای نسبت کرنش اصلی در معادلات جایگذاری شود، یعنی:
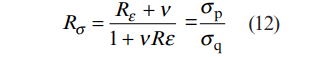
یا
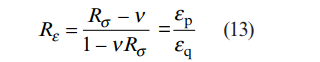
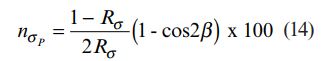
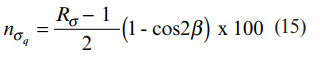
بررسی خطاها و حساسیت عرضی گیج ها
حساسیت عرضی در استرین گیج به رفتار گیج در پاسخ به کرنش هایی که بر محور اصلی حسگر عمود هستند اشاره دارد. در این مقاله با این نوع خطا بیشتر آشنا خواهید شد.

اکنون معادلات (11)، (14) و (15) برای نشان دادن میزان بزرگی خطاهای به وجود آمده، برای یک مثال نوعی حل خواهد شد.
ابتدا یک مخزن فشار استوانه ای دیواره نازک را در نظر بگیرید. در این حالت تنش حلقه یا تنش محیطی دو برابر تنش طولی و با علامت یکسان است.
بدین ترتیب:
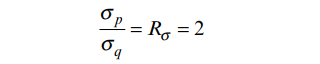
در این حالت روابط (11) ، (14) و (15) را می توان به شکل زیر بازنویسی کرد:
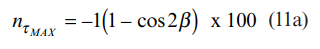
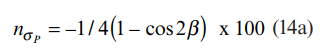
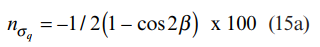
معادلات (11a) ، (14a) و (15a) در شکل 5 ترسیم شده اند. از این شکل می توان دریافت که خطاهای ایجاد شده توسط
ناهمترازی روزت در این مثال بسیار کوچک است. به عنوان مثال، با خطای نصب 5 درجه،
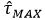 ،
، 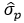 و
و
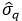 به ترتیب تنها 1.5%- ، 0.38%- و 0.75% هستند.
به ترتیب تنها 1.5%- ، 0.38%- و 0.75% هستند.
برای تصحیح خطای ناشی از نصب غیر صحیح روزت برای زاویه های معلوم، ابتدا باید مقدار n از شکل 5 یا از
نمودارهای مشابه که از معادلات اصلی [(7) ، (9)، (11)، (14)، (15)] استخراج شده است، خوانده شود و سپس
معادلات (6)، (8) و (10) با جایگذاری n خوانده شده به همراه علامت آن از شکل 5، به ترتیب برای پارامترهای
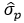 ،
، 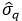 و
و
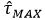 حل شوند. یعنی:
حل شوند. یعنی:



که در آن :
: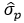 ماکزیمم تنش اصلی که از قرائت های گیج محاسبه شده است.
ماکزیمم تنش اصلی که از قرائت های گیج محاسبه شده است.
: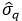 مینیمم تنش اصلی که از قرائت های گیج محاسبه شده است.
مینیمم تنش اصلی که از قرائت های گیج محاسبه شده است.
: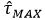 ماکزیمم تنش اصلی برشی که از
ماکزیمم تنش اصلی برشی که از
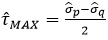 به دست آمده است.
به دست آمده است.
با اینکه خطاهای محاسبه شده در مثال بالا کوچک بودند، این قضیه برای تنش هایی که Rσ بزرگی دارند،
صادق نیست. در حالت کلی مقدار 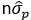 برای مقادیر
برای مقادیر
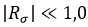 بسیار بزرگ می باشد. این برای
بسیار بزرگ می باشد. این برای
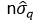 با
با 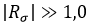 صادق است. خطا در تنش برشی مستقل از حالت تنش می باشد.
صادق است. خطا در تنش برشی مستقل از حالت تنش می باشد.
مطالب پیشنهادی برای شما

پایه و اساس پل وتستون
در این مقاله شما با نحوه عملکرد مدار پل وتستون به همراه روابط کامل آن در مبدل های استرین گیجی آشنا خواهید شد

خزش و پسماند گیج ها
در این مقاله شما با خطای خزش و همچنین خطای پسماند برای استرین گیج های مختلف آشنا خواهید شد.

خطای ناهمترازی گیج ها
اگر گیج در راستای مورد نظر به درستی نصب نشود، باعث بروز خطاهایی خواهد شد، در اینجا با این خطاها آشنا خواهید شد

حساسیت عرضی گیج ها
در این مقاله با جزئیات به بررسی خطاهای ناشی از حساسیت عرضی استرین گیج های مختلف پرداخته شده است.